1. Что такое дерево решений.

Рассмотрим следующий пример задачи распознавания. Пусть при первичном осмотре некоторого числа ЛОР - пациентов определены следующие их характеристики: - температура, - наличие кашля, - наличие покраснения горла, ={простуда, ангина, грипп, пневмония, здоров} – набор из возможных диагнозов, требующих более углубленного обследования.

Требуется найти модель зависимости Y от Х. На рис.1 изображен (иллюстративный) пример такой модели, заданный в виде дерева решений.

Обыкновенное дерево состоит из корня, ветвей, узлов (мест разветвления), листьев. Точно также дерево решений состоит из узлов (называемых также вершинами), обозначаемых окружностями; ветвей, обозначаемых отрезками, соединяющими узлы. Для удобства дерево решений изображают обычно слева направо или сверху вниз. Самая первая (левая или верхняя) вершина называется корнем. Цепочка "корень - ветвь - вершина - ... - вершина" заканчивается вершиной, которую называют "листом". Из каждой внутренней вершины (т.е. не листа) может выходить две или более ветвей. Каждому такому узлу сопоставлена некоторая характеристика, а ветвям - области значения этой характеристики, причем эти области дают разбиение множества значений данной характеристики.

В случае, если из каждой внутренней вершины выходит ровно две ветви (дерево такого типа называется дихотомическим), каждой ветви можно сопоставить истинность или ложность некоторого утверждения относительно данной характеристики, как это изображено для фрагмента дерева на рис.2.

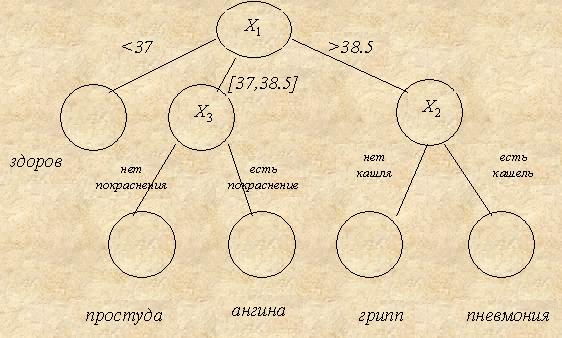
Рис.1

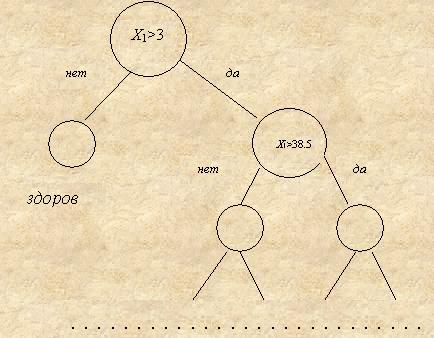
Рис.2

Каждой конечной вершине дерева (листу) приписано решение – некоторое значение Y. В случае задачи распознавания образов данное значение - это определенный класс, а в случае регрессионного анализа – некоторое число. Деревья решений для задачи кластер-анализа будут рассматриваться особо в параграфе 4.

Для любого наблюдения х, используя дерево решений, мы можем найти прогнозируемое значение Y. Для этого начинают с корня дерева; рассмотрим характеристику, сопоставленную корню и определим, какой из ветвей соответствует наблюдаемое значение данной характеристики. Рассмотрим теперь вершину, в которую привела данная ветвь. Для этой вершины повторим аналогичные действия и т.д., пока не придем к листу. Значение Y^S, приписанное S-му листу, и будет являться прогнозом для x. Таким образом, дерево решений дает модель T зависимости Y от X: Y=T(X).

Деревья решений, рассматриваемые в задаче регрессионного анализа, называют также деревьями регрессии.

В данном пособии мы будем рассматривать самый простой вид деревьев решений, описанный выше. Существуют, однако, более сложные виды деревьев, каждой внутренней вершине которых соответствуют более сложные высказывания о значениях не одной, а нескольких характеристик. Например, эти высказывания могут определяться линейной комбинацией количественных характеристик (например, выражением 10x₁+5x₂–1>0), т.е. соответствовать различным подобластям разбиения гиперплоскостью многомерного пространства). С этой точки зрения рассматриваемому нами варианту деревьев решений соответствуют гиперплоскости, перпендикулярные числовым осям.

Дерево решений должно быть непротиворечивым, т.е. на пути, ведущем из корня в лист, не должно быть взаимно исключающих вариантов, например «X₁ > 37» и «X₁ < 30».

Можно выделить следующие особенности деревьев решений.

Деревья решений позволяют обрабатывать одновременно как количественные, так и качественные характеристики.

Дереву решений соответствует набор логических высказываний о значениях характеристик. Каждое высказывание получается при прохождении пути из корневой вершины в лист. Так, например, дереву, изображенному на рис. 1 соответствует следующий список высказываний:

1. Если , То Y=«здоров».

2. Если И X₃=«нет покраснения горла», То Y=«простуда»;

3. Если И X₃=«есть покраснение горла», То Y=«ангина»;

4. Если И X₂=«нет кашля», То Y=«грипп»;

5. Если И X₂=«есть кашель», То Y=«пневмония»;

Таким образом, дерево решений представляет собой логическую модель закономерностей исследуемого явления.

К недостаткам деревьев решений можно отнести то, что в случае, когда все характеристики являются количественными, дерево решений может представлять собой довольно грубое приближение к оптимальному решению. Например, дерево регрессии, изображенное на рис.3, является кусочно-постоянным приближением к регрессионной функции. С другой стороны, этот недостаток можно отчасти компенсировать увеличением числа листьев, т.е. уменьшением длины соответствующих «кусков» или «ступеней».

Рассмотрим дерево решений с M листьями. Этому дереву будет соответствовать разбиение пространства характеристик на М попарно непересекающихся подобластей Е¹,...,E^M, так что каждому S-му листу сопоставляется подобласть Е^S (рис. 4). Как образуется данная подобласть?

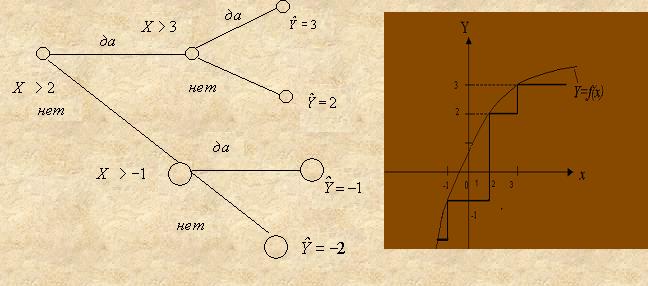
Рис.3

Е^S определяется декартовым произведением Е^S =, где – проекция Е^S на j-ю характеристику. получается следующим образом. Если характеристика не встречается ни разу на пути, ведущим из корня в S-й лист, то совпадает с областью определения характеристики . В противном случае равно пересечению всех подобластей характеристики , встретившихся на пути из корня в S-й лист.

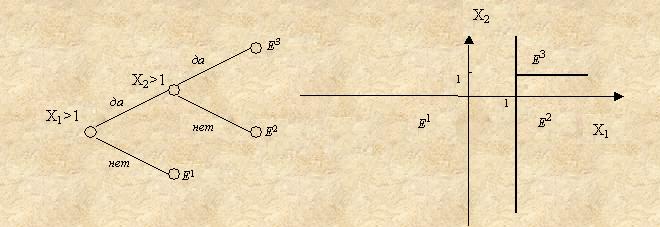
Рис.4

Пусть имеется некоторый набор наблюдений Data=(xⁱ,yⁱ), i=1,...,N. Каждое из этих наблюдений принадлежит (по Х) какой-либо из рассматриваемых подобластей, т.е. . Множество наблюдений, принадлежащих Е^S , обозначим Data^S, а число таких наблюдений обозначим N ^S. Пусть обозначает число наблюдений из Data^S, принадлежащих i-му классу (задача РО).

Вернуться в оглавление