2. Как
строятся деревья решений.
Процедуру формирования
дерева решений по статистическим данным принято также называть построением
дерева. В этом параграфе мы познакомимся с некоторыми способами построения деревьев,
а также способами определения качества дерева решений.
Для каждой конкретной задачи статистического анализа существует большое число (часто даже бесконечно много) различных вариантов деревьев решений. Возникает вопрос: какое именно дерево лучше и как его найти. Чтобы ответить на первую часть вопроса, рассмотрим различные способы определения показателей, характеризующих качество дерева. В идеале основным показателем может служить ожидаемая погрешность прогнозирования. Однако эту величину можно определить, лишь зная вероятностный закон распределения исследуемых переменных. На практике этот закон, как правило, неизвестен. Поэтому качество можно только приближенно оценить, используя данный нам набор наблюдений.
2.1 Показатели качества дерева.
Предположим, что имеется
некоторое дерево решений, а также выборка объектов наблюдения объема N.
Можно выделить два основных вида показателей, характеризующих качество дерева.
Первый вид - это показатели точности, второй вид - показатели сложности дерева.
Показатели точности дерева
определяются с помощью выборки и характеризуют то, насколько хорошо разделены
объекты разных классов (в случае задачи распознавания), либо то, насколько
велика погрешность прогнозирования (в случае задачи регрессионного анализа).
Относительное число
(частота) ошибок представляет собой долю объектов, неверно отнесенных деревом к
чужому классу:
,
где
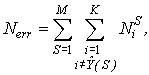
где K – число классов.
Относительную дисперсию для
дерева регрессии можно рассчитать по формуле: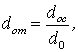 
где
– остаточная дисперсия,
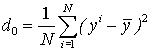
– исходная дисперсия,
.
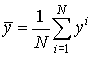Показатели сложности дерева
характеризуют его форму безотносительно к выборке.
К этим показателям относятся
число листьев дерева, число его внутренних вершин, максимальная длина пути из
корня в конечную вершину.
Может также использоваться
длина внешнего пути, которая определяется как число ветвей, дополняющих данное
дерево до полного дерева, т.е. от такого дерева, в котором все пути из корня к
листьям имеют одинаковую длину.
Показатели сложности и
точности взаимосвязаны: чем сложнее дерево, тем оно, как правило, точнее (если
рассмотреть дерево, в котором каждому листу соответствует один объект, то
точность будет максимальной).
Менее сложное дерево, при
прочих равных условиях, более предпочтительно. Это объясняется стремлением
получить более простую модель исследуемого явления, облегчить последующую
интерпретацию («объяснение» модели). Кроме того, из теоретических исследований
следует, что в случае небольшого (в сравнении с числом характеристик) объема
выборки слишком сложное дерево становится неустойчивым, т.е. дает более высокую
погрешность для новых наблюдений.
С другой стороны, понятно,
что чересчур простое дерево также не позволит достичь хороших результатов
прогнозирования. Таким образом, при выборе наилучшего дерева решений должен
достигаться определенный «компромисс» между показателями точности и сложности.
Для получения такого компромиссного
варианта можно использовать, например, следующий критерий качества дерева: 
, где p -показатель точности, 
– некоторый заданный
параметр. Наилучшее дерево соответствует минимальному значению данного
критерия.
Используется также подход,
при котором заранее задается максимально допустимая сложность дерева, при этом
ищется наиболее точный вариант.