2.3 Методы построения деревьев решений.

Существующие методы (всего их несколько десятков), в принципе, могут быть разделены на две основные группы. К первой группе относятся методы построения строго-оптимального по заданному критерию качества дерева, ко второй группе – методы построения приближенно-оптимального дерева.

Задачу поиска оптимального варианта дерева можно отнести к задаче дискретного программирования или выбора из конечного (но очень большого) числа вариантов. Это следует из того, что для конечной обучающей выборки число вариантов ветвления (см. ниже) по каждой характеристике конечно.

В дискретном программировании рассматриваются три основные вида методов: полный перебор, метод динамического программирования и метод ветвей и границ. Однако эти методы, в приложении к деревьям решений, как правило, являются очень трудоемкими, особенно при большом числе наблюдений и характеристик. Поэтому мы ограничимся приближенными методами, к числу которых относятся метод последовательного ветвления, метод усечения и рекурсивный метод.

Рассмотрим сначала основные операции с деревьями решений. Методы построения деревьев будут представлять собой определенную последовательность этих операций.

2.3.1 Операция ветвления (разделения).

Данная операция является основной при построении дерева. Рассмотрим некоторую вершину дерева и произвольную характеристику X_j. Пусть область определения этой характеристики разделена (разбита) на L_j подмножеств (способы выбора таких подмножеств рассмотрим ниже). В случае количественной характеристики эти подмножества представляют собой набор подынтервалов разбиения, в случае качественной характеристики - произвольные подмножества значений, а в случае порядковой характеристики - подмножества, включающие соседние по порядку значения.

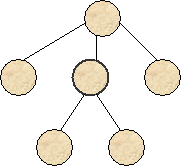
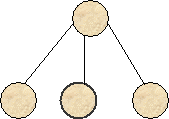
Сопоставим каждому из этих подмножеств ветвь дерева, выходящую из данной (родительской) вершины и ведущую в новую вершину-потомок. Таким образом, вершина "разветвилась" ("разделилась") на L_j новых вершин (рис. 5).

Рис.5

Заметим, что для дихотомических деревьев L_j всегда равно двум. Если L_j всегда равно трем, то такие деревья называют тернарными. Если L_j всегда равно четырем, то получим квадро-деревья.

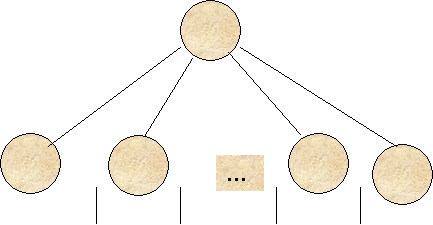
Как получить разбиение области определения? Возьмем множество наблюдений, соответствующих данной вершине и рассмотрим значения характеристики X_j для этих наблюдений.

Рис.6

Пусть характеристика – количественная. В этом случае определяются границы – середины интервалов между соседними значениями, и разделение проводится по этим границам (рис.6). Например, для примера на рис. 7 (значения характеристики для наблюдений обозначены через «), в случае дихотомического дерева, можно рассматривать следующие варианты разделения: X_j < 0.5 или X_j >=0.5, X_j < 1.5 или X_j >=1.5. Если характеристика -–качественная, то варианты разбиения получаются непосредственно по значениям характеристики, например если X_j означает страну, то может быть получено следующее разбиение: X_j 0{Канада, Мексика, США} или X_j 0{Аргентина, Бразилия}.

Рис.7

При наличии большого числа значений число возможных вариантов становится чересчур большим, поэтому для ускорения процесса построения дерева рассматривают не все варианты, а только некоторые из них (например, такие как X_j =«Канада» или X_j≠ «Канада»).

В случае порядковой характеристики варианты разбиения состоят из соседних по порядку значений, например если X_j – воинское звание, то разделение может быть такое: X_j0[рядовой – старшина] или X_j0 [лейтенант – майор].

В некоторых случаях (при малом числе наблюдений) для качественных или порядковых характеристик может случиться так, что множество значений характеристик для наблюдений, соответствующих вершине, составляет лишь часть всей области определения этой характеристики. В этом случае необходимо оставшиеся значения, по какому- либо правилу приписать какой-либо из новых ветвей. Это нужно для того, чтобы при прогнозировании для объекта контрольной выборки, у которого встретилось такое значение, определить, к какой из ветвей он относится. Например, можно приписать данные значения той ветви, которой соответствует наибольшее число наблюдений.

2.3.2 Операция определения перспективности дальнейшего ветвления вершины (правило остановки).

Рассмотрим висячую вершину дерева, т.е. вершину, из которой не выходят ветви, но не ясно, будет ли эта вершина листом или произойдет дальнейшее ветвление. Рассмотрим подмножество наблюдений, соответствующее данной вершине. Вершина относится к бесперспективным для дальнейшего ветвления в двух случаях. Во-первых, если эти наблюдения однородны, т.е. в основном принадлежат к одному классу (задача распознавания образов, РО), либо разброс значений Y для них достаточно мал (задача регрессионного анализа, РА). К этому случаю относится и вариант, когда у наблюдений совпали значения всех X-ов. Во-вторых, если число наблюдений достаточно мало.

Вершина, бесперспективная для дальнейшего ветвления, объявляется листом.

Для определения перспективности можно задать следующие параметры: допустимую ошибку для вершины (задача РО), допустимую дисперсию (задача РА), порог на число наблюдений.

2.3.3 Операция присваивания решения листу.

Рассмотрим произвольный лист дерева. Этому листу соответствует подмножество наблюдений Data'. При решении задачи распознавания образов листу присваивается тот класс, для которого количество наблюдений из Data' максимально, в сравнении с другими классами. При решении задачи регрессионного анализа решение, присвоенное листу, равно среднему значению зависимой характеристики Y для наблюдений из Data'.

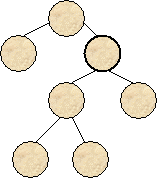
2.3.4 .Операция "разрастания" вершины.

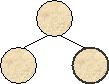
Эта операция представляет собой последовательность операций ветвления для каждой из новообразованных вершин дерева. В результате этой операции данная вершина заменяется некоторым поддеревом (т.е. частью полного дерева, которая также имеет вид дерева (рис.8)).

Рис.8

Сложность поддерева ограничивается некоторым параметром. Подробнее один из способов разрастания будет описан ниже.

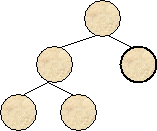
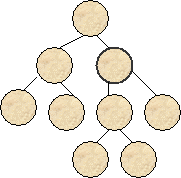
2.3.5. Операция усечения.

Эта операция обратна операции разрастания, т.е. для данной вершины полностью отсекается соответствующее поддерево, для которого эта вершина является корнем (рис. 9). Вершина затем объявляется листом и ей присваивается решение.

Рис.9

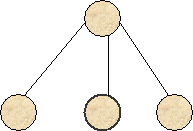
2.3.6. Операция "срастания" вершин или ("склейки").

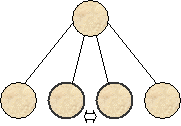
Пусть вершина разделилась на L новых вершин. Возьмем какую-либо пару этих вершин и объединим их в одну вершину, которую соединим с родительской вершиной веткой (рис. 10). При этом подмножества значений, соответствующие срастаемым вершинам, объединяются.

Рис.10

Для количественных и порядковых характеристик допускается срастание вершин, которым соответствуют соседние подынтервалы или подмножества значений характеристик.

Вернуться в оглавление