2.4 Критерии качества ветвления.

При сравнении различных вариантов ветвления некоторой вершины необходим критерий, который позволял бы сравнивать эти варианты и выбирать наилучший из них.

Таким критерием может являться частота ошибок (в задаче РО) или относительная дисперсия (в задаче РА). Пусть вершина разделилась на L новых вершин; обозначим через число наблюдений, соответствующее l-й новой вершине, Data_l – множество этих наблюдений, - решение, приписанное l-й вершине, - число наблюдений класса ω, которые соответствуют l-й вершине (задача РО). Общее число наблюдений в исходной вершине обозначим N. Формулы для вычисления критериев аналогичны тем, которые использовались при определении качества дерева решений (т. к. вариант ветвления также представляет собой дерево):

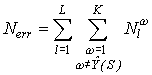
(для задачи РО);

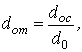
где

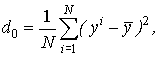
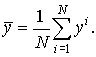
Для задачи РО существуют и более тонкие способы определения того, насколько хорошо разделены объекты разных классов (в зарубежной литературе используется термин "impurity", который можно интерпретировать как степень "загрязнения" наблюдений "чужими" классами). Рассмотрим, для примера, два варианта разделения (рис. 11).

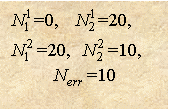
Рис.11

Число ошибок для этих вариантов совпадает, однако ясно, что первый вариант более предпочтителен, т.к. в нем одна из новых вершин уже не нуждается в дальнейшем ветвлении, поскольку все объекты в ней безошибочно отнесены к одному классу.

Чтобы учитывать подобные случаи, для определения качества разделения можно использовать критерий энтропии или индекс Гини.

Критерий энтропии разбиения определяется по формуле:

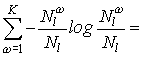
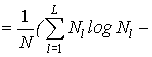
Чем меньше значение энтропии, тем больше информации содержится в варианте разделения. Если обозначить

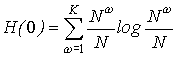
энтропию для исходной вершины, где означает число наблюдений класса ω, то в качестве меры «полезности» или «выигрыша», которое дает данное ветвление, можно использовать величину gain=H(L)-H(0).

Можно указать следующие свойства энтропийного критерия:

1) При постоянном числе классов, значение H увеличивается, если частоты различных классов сближаются друг к другу.

2) Если различные классы равновероятны, а число классов увеличивается, то H увеличивается с логарифмической скоростью (т.е пропорционально логарифму K).

Основанием логарифма в вышеуказанных формулах служит 2. Кроме того, в некоторых исследованиях рекомендуется использование в качестве основания величины L.

Индекс Гини для разбиения вычисляется по следующей формуле:

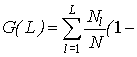
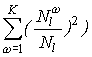
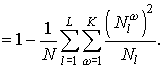
Меньшее значение этого показателя также соответствует лучшему разделению объектов.

Кроме того, для определения качества также используют показатель «выигрыша» ("gain") ветвления, который определяется как разница между значениями данного критерия для исходной вершины и варианта ее разделения.

Вернуться в оглавление