2.8 Оценивание качества и сравнение методов.
При оценивании качества
метода построения деревьев решений необходимо учитывать такие показатели, как
трудоемкость, требуемые системные ресурсы компьютера (оперативная и дисковая
память). В то же время основным, наиболее важным показателем качества служит
погрешность прогнозирования.
Как было сказано выше, наиболее объективным способом определения погрешности является способ, основанный на использовании контрольной выборки. Этот способ можно применять при обработке больших баз данных, состоящих из сотен или тысяч наблюдений. Однако при анализе данных сравнительно небольшого объема разделение выборки на обучающую и контрольную может привести к нежелательным последствиям, так как теряется часть информации, которая могла бы быть использована при построении дерева. Кроме того, оценка качества будет зависеть от способа разбиения выборки на обучающую и контрольную. Для уменьшения влияния этой зависимости можно использовать методы, основанные на многократном повторении процедуры разбиения и последующем усреднении полученных оценок качества.
Метод скользящего экзамена. В этом методе поочередно
каждый объект выборки «выбрасывается» из нее, по оставшейся части выборки
строится дерево, с помощью которого затем находится прогноз для данного
объекта. Прогнозируемое значение сравнивается с наблюдаемым, после чего объект
возвращается в исходную выборку. Процент ошибок (в случае задачи РО) или
средний квадрат погрешности (в случае задачи РА) показывает качество метода.
Этот метод является довольно
трудоемким, так как необходимо решить N задач построения дерева решений (N -
объем выборки).
Метод L-кратной перекрестной
проверки ("L-fold cross-validation"). В этом методе исходная
выборка случайным образом делится на L частей, приблизительно одинаковых по
объему. Затем каждая часть поочередно выступает как контрольная выборка, а
оставшиеся части объединяются в обучающую. Показателем качества метода служит
усредненная по контрольным выборкам ошибка. Данный метод менее трудоемкий, чем
метод скользящего экзамена, а при уменьшении параметра L приближается к этому
методу.
При сравнении различных
методов построения деревьев решений важное значение имеют данные, по которым
строятся деревья. По способу получения эти данные можно разделить на две группы.
В первую группу входят реальные данные, предназначенные для решения какой-либо
конкретной прикладной задачи. Для удобства сравнения различных методов эти
данные хранят в специальных базах данных, доступных через сети Интернет
(например, UCI Machine
Learning Database Repository
http://www.ics.uci.edu/~mlearn/MLRepository.html).
Во вторую группу входят данные, искусственно сгенерированные согласно какому-либо алгоритму. При этом распределение («структура») данных в пространстве характеристик известно заранее, что позволяет точно определить качество каждого метода в зависимости от вида распределения, объема обучающей выборки и числа характеристик. В качестве примера, рассмотрим данные, имеющие «структуру шахматной доски» (рис. 17). Белым клеткам соответствует первый класс (x), а черным – второй (0). Кроме характеристик X1 и X2, имеются еще «шумовые» характеристики X3 и X4 (по которым каждый класс имеет равномерное распределение).
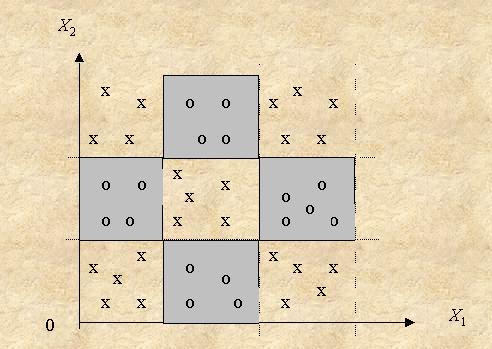
Рис. 17
Сравнение описанных выше
методов показало, что только рекурсивный метод позволил построить дерево
решений, правильно определяющий задуманную структуру.
Вообще же говоря, многочисленные
сравнения существующих методов показывают, что нет «универсального» метода,
который одинаково хорошо работал бы на любых данных.