4. Деревья решений в задачах кластер-анализа и анализа временных
рядов.
В предыдущих параграфах рассматривались задачи
регрессионного и дискриминантного анализа (распознавания образов). Кроме этих
задач, на практике часто возникают и другие виды задач многомерного
статистического анализа. В этом параграфе мы рассмотрим задачи кластер-анализа
и анализа многомерных временных рядов, которые также могут быть решены при
помощи деревьев решений. При этом все положительные черты методов, основанных
на деревьях решений (возможность обработки как количественной, так и
качественной информации, простота интерпретации) также относятся и к этим новым
задачам.
4.1. Кластер-анализ с использованием деревьев
решений.
При решении задачи кластер-анализа («таксономии»,
«автоматической группировки объектов по похожести их признаков») задача состоит
в следующем. Используя результаты наблюдений, требуется разбить исходное
множеств наблюдаемых объектов на заданное число (или, быть может, на не более
чем) K групп («кластеров») так, чтобы объекты внутри каждой группы были бы в
определенном смысле «похожи» друг на друга, в то время как объекты разных групп
были бы как можно более различными. Это необходимо для того, чтобы лучше понять
структуру данных, заменив большое число исходных объектов относительно
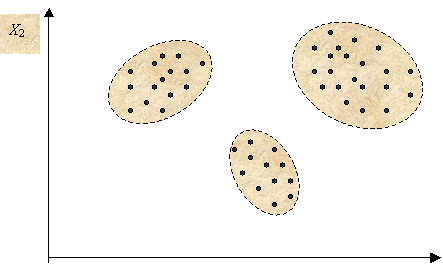
небольшим числом групп схожих объектов (рис. 19). Слово «кластер» можно
перевести как «гроздь», «скопление».
Рис. 19
Таким образом, требуется обнаружить такие
«скопления» объектов в пространстве характеристик, которые наилучшим образом
удовлетворяли бы некоторому критерию качества группировки. Предполагается, что
характеристики, описывающие объекты, могут быть как количественными, так и
качественными. Различные методы кластер-анализа отличаются способами понимания
похожести, критерием качества и способами нахождения групп.
Будем решать задачу, используя деревья решений.
Сначала определим критерий качества группировки, соответствующей дереву. Как
было отмечено в параграфе 1.1, дерево решений с М
листьями задает разбиение пространства характеристик на М попарно непересекающихся подобластей Е1,...,EM, которому, в свою очередь, соответствует разбиение
всего множества наблюдений Data на М подмножеств Data1,...,DataM.
Таким образом, число листьев в дереве совпадает с числом подмножеств (групп)
объектов: K=M. Рассмотрим произвольную группу объектов Datai.
Описанием этого подмножества назовем следующую
конъюнкцию высказываний: S(Datai,
)=«X1 
» И «X2 
» И ... И «Xj 
» И ... И «Xn 
», где 
– отрезок 
=[
, 
] в случае количественной характеристики Xj, либо
множество принимаемых значений 
в случае качественной характеристики.
Подобласть пространства характеристик 
, соответствующую описанию группы, назовем таксоном.
В примере на рис. 20 плоскость разбита с помощью
дерева на три подобласти.
Рис.20
S(Data1,
)=«X1 
[1,4]» И «X2 
[4,6]»;
S(Data2,
)=«X1 
[9,13]» И «X2 
[4,6]»;
S(Data3,
)=«X1 
[11,13]» И «X2 
[1,3]».
Важно отметить, что хотя и в дереве решений может
использоваться лишь часть характеристик, в описании каждой группы участвуют
обязательно все имеющиеся характеристики.
Относительной мощностью (объемом) таксона назовем
величину
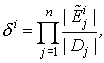
где
символом 
обозначена длина интервала (в случае количественной
характеристики) либо мощность (число значений) соответствующего подмножества 
(в случае
качественной характеристики); |Dj| - длина интервала между минимальным и
максимальным значением характеристики Xj для всей исходной выборки объектов (для
количественной характеристики) либо общее число значений этой характеристики
(для качественной характеристики).
Под критерием качества группировки, при заданном
числе кластеров, будем понимать величину суммарного относительного объема
таксонов:
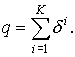
Оптимальной
группировкой будем считать группировку, для которой значение
данного критерия минимально.
Если же число кластеров заранее не задано, под
критерием качества можно понимать величину
, где 
>0 - некоторый
заданный параметр. При минимизации этого критерия, с одной стороны, мы получаем
таксоны минимального объема, а с другой стороны, стремимся уменьшить число этих
таксонов.
Заметим, что в случае, когда все характеристики
количественные, минимизация критерия означает минимизацию суммарного объема
многомерных параллелепипедов, «охватывающих» группы.
Для построения дерева может использоваться
описанный в параграфе 2.3.3 метод последовательного ветвления, на каждом шаге
которого некоторая группа объектов, соответствующая висячей вершине дерева,
разделяется на две новых подгруппы.
Разделение происходит с учетом критерия качества
группировки, т.е. минимизируется суммарный объем полученных таксонов.
Перспективной для дальнейшего ветвления считается вершина, для которой объем
соответствующего таксона больше наперед заданной величины. Разделение
продолжается до тех пор, пока не останется более перспективных вершин, либо не
будет получено заданное число групп.
Кроме этого метода, может также использоваться и
рекурсивный метод, описанный в параграфе 2.3.4. Для этого метода используется
второй вариант критерия качества группировки Q, для
которого число групп заранее не задано. Все шаги алгоритма построения дерева
остаются без изменения, с той лишь поправкой, что используется данный критерий
качества. Можно заметить, что при построении «начального» дерева образуется
большое число таксонов небольшого объема, которые затем при проведении операции
«склейки» как бы «сливаются» в один или несколько более объемных таксонов так,
чтобы улучшить критерий качества группировки.