4.2. Деревья решений и анализ многомерных временных рядов.

В этом разделе мы рассмотрим методы решения задач анализа и прогнозирования многомерных разнотипных временных рядов.

Во многих практических задачах требуется прогнозировать значения характеристик некоторого объекта на основе анализа их значений в предыдущие моменты времени.

В настоящее время разработана теория и создано большое число различных методов анализа многомерных числовых последовательностей. Однако применение этих результатов для решения рассматриваемой задачи в случае разнотипных характеристик невозможно (так как для качественных характеристик не определены арифметические операции на множестве их значений).

Использование деревьев решений позволяет решать указанные задачи.

Пусть для описания некоторого объекта исследования используется набор случайных характеристик X(t)=(X₁(t),...,X_n(t)), значения которых меняются с течением времени. Характеристики могут быть как количественными, так и качественными.

Пусть характеристики измеряются в последовательные моменты времени t¹,..., t^μ,... . Для определенности будем предполагать, что измерения проводятся через равные интервалы времени. Обозначим через x_j(t^μ)=X_j(t^μ) значение характеристики X_j в момент времени t^μ. Таким образом, имеем n-мерный разнотипный временной ряд x_j(t^μ), j=1,...,n, μ=1,2,....

Пусть выбрана некоторая прогнозируемая характеристика X_j0, 1#j₀#n

Обозначим, для удобства, эту характеристику через Y. Характеристика Y может быть как количественной, так и качественной.

Рассмотрим произвольный момент времени t^μ, а также набор предыдущих моментов времени t^μ-1, t^μ-2,…, t^μ-l , где l - некоторая заданная величина (лаг или «глубина предыстории»), 1<l<:. Будем полагать, что условное распределение Y(t^μ) при условии, что заданы все предыдущие значения X(t) зависит только от значений ряда в l предыдущих моментов времени.

Кроме того, предположим, что эта зависимость одна и та же для любых μ. Данное предположение означает, что статистические свойства ряда, определяющие зависимость, неизменны во времени.

Для произвольного момента времени t^μ можно образовать набор v^μ=(X_j(t^μ-i)), i=1,...,l, j=1,...,n, представляющий собой реализации временного ряда в l предшествующих моментов времени. Набор v^μ назовем предысторией длины l для момента t^μ.

Требуется построить модель зависимости характеристики Y от ее предыстории для произвольного момента времени. Модель позволяет прогнозировать значение характеристики Y в будущий момент времени по значениям характеристик за l прошлых моментов. Иначе говоря, данная модель представляет собой решающую функцию для прогнозирования по предыстории.

В зависимости от типа характеристики Y можно рассматривать различные типы задач прогнозирования.

1. Y – качественная характеристика. Задачу данного типа, по аналогии с обычной задачей распознавания образов, назовем задачей распознавания динамического объекта. Анализируемый объект может с течением времени менять соответствующий ему образ.

2. Y – количественная характеристика: В этом случае имеем задачу прогнозирования количественной характеристики объекта.

Решающую функцию для прогнозирования временного ряда по его предыстории будем представлять в виде дерева решений. Это дерево решений отличается от описанного в параграфе 2 только тем, что в нем проверяются высказывания относительно некоторых характеристик X_j в некоторый i-й отсчет времени назад. Для удобства, будем обозначать эти характеристики, с учетом предыстории, через X_jⁱ (рис. 21). Таким образом, X_jⁱ означает «характеристика X_j в i-й предыдущий момент времени (относительно текущего момента).

Итак, пусть имеется набор измерений характеристик X=(X₁,...,X_n) в моменты времени t¹,...,t^N и задано значение l. Таким образом, имеем многомерный разнотипный временной ряд длины N. Сформируем множество всех предысторий длины l для моментов времени t^l+1,...,t^N: A= v^μ , μ=l+1,...,N.

Для любого заданного дерева решений для прогнозирования по предыстории можно определить его качество аналогично тому, как это делалось

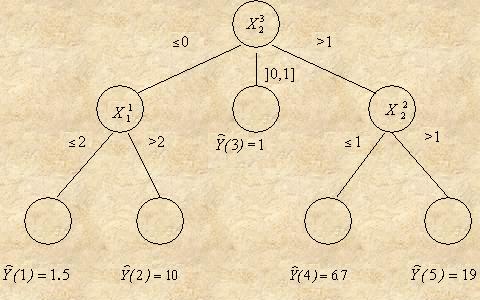
Рис. 21

для обычного дерева: обозначим через прогнозируемое значение Y, полученное с помощью дерева по предыстории v^μ , тогда критерий качества будет

,

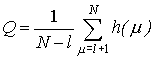где

– для задачи распознавания динамического объекта;

– для задачи прогнозирования количественной характеристики.

Будем говорить, что данный ряд используется для «обучения» прогнозированию.

Пусть имеется ряд x(t^μ) длины N_c, μ=N+1,...,N+N_c. Тогда можно сравнить полученные в результате обучения прогнозируемые значения с «истинными» значениями и определить погрешность прогноза. В этом случае будем говорить, что данный ряд используется для «контроля» качества прогнозирования.

Как построить по имеющемуся временному ряду дерево решений для прогнозирования по предыстории? Ниже описывается несколько способов, при использовании которых исходная задача построения дерева решений разбивается на ряд более простых задач распознавания образов или регрессионного анализа, в зависимости от типа прогнозируемой характеристики Y.

Набор v^μ представим в виде таблицы v^μ =(X_j(t^μ-i), i=1,...,l, j=1,...,n, содержащей l строк и n столбцов. Тогда исходной информацией для прогнозирования является набор таблиц v^μ, вместе с указанными для каждой таблицы значениями прогнозируемой характеристики Y(t^μ), μ=l+1,...,N.

Mножество A= v^l+1,…, v^N можно представить в виде трехмерной таблицы размерности l´n´(N–l), которой будет соответствовать вектор (y^l+1,...,y^N) (рис. 22). Однако имеющиеся методы распознавания или регрессионного анализа с использованием деревьев решений используют в качестве входной информации двумерные таблицы.

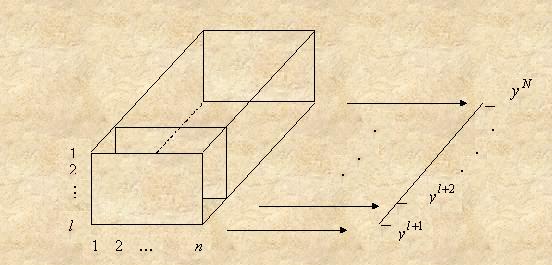
Рис. 22

Можно указать несколько различных способов использования данных методов для решения задачи анализа трехмерных таблиц данных.

1. Каждая таблица v^μ представляется в виде строки соответствующих значений характеристик , μ=l+1,...,N (иначе говоря, таблица просто «вытягивается» в строку).

В результате получаем двумерную таблицу размерности l´n´(N–l), для которой затем строится решающая функция, представленная в виде дерева решений. Для этого может использоваться один из методов, описанных в параграфе 2.

Данный способ очень прост в реализации, однако, как показывают исследования, полученные решения, в условиях большого числа характеристик, большой длины предыстории и сравнительно малой длины ряда, могут оказаться неустойчивыми, т.е. будут давать большую ошибку на контрольном ряде (известно, что эффект неустойчивости проявляется при малом объеме выборки и большом числе характеристик).

2. Исходная задача решается в два этапа. На первом этапе рассматриваются l двумерных таблиц вида (X_j(t^μ-i),Y(t^μ)), где j принимает значения 1,...,n, μ – значения l+1,...,N, i – значения 1,...,l, образованных «горизонтальными» срезами исходной трехмерной таблицы данных (рис. 23).

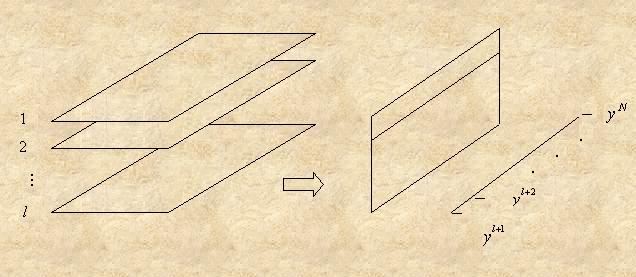
Рис. 23

Строятся l различных деревьев решений для предсказания величины Y по каждой из данных таблиц. Каждая из таблиц, с помощью построенного дерева, «свертывается» в одномерную строку символов (каждый символ кодируется номером соответствующей конечной вершины дерева). Таким образом, получается двумерная таблица, для которой на втором этапе снова строится дерево решений. Затем каждый символ обратно преобразуется в соответствующую цепочку высказываний.

3. Задача решается также в несколько этапов.

1) Рассматриваются l таблиц вида , где j принимает значения 1,...,n, μ – значения l+1,...,N, i – значения 1,...,l , и затем n таблиц вида , где i принимает значения 1,...,l, μ – значения l+1,...,N, j – значения 1,...,n. Таким образом, имеем l «горизонтальных» и n «вертикальных» срезов исходной таблицы (рис. 24).

Для каждой из полученных двумерных таблиц строится дерево решений. В итоге получаем набор деревьев T₁,T₂,..., T_l+n. Обозначим через наилучшее из этих деревьев.

2) Рассматриваются все конечные вершины дерева и выделяются те из них, для которых ошибка прогнозирования превышает заданную величину. Для каждой из этих вершин формируется соответствующий набор

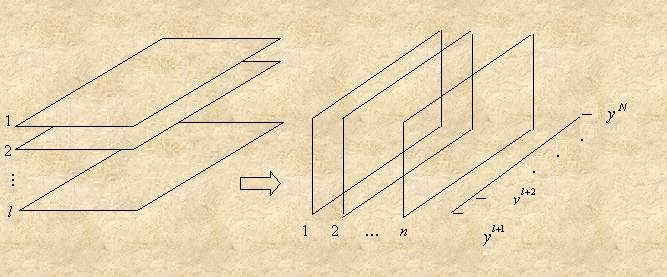
Рис. 24

предысторий , и далее процесс достраивания дерева для повторяется, начиная с п.1).

3) Процесс продолжается до тех пор, пока на некотором шаге полученное дерево не будет удовлетворять условию окончания (т.е. если число конечных вершин достигнет определенной величины M_max, либо ошибка прогнозирования станет меньше заданного значения).

Можно заметить, что данный способ отличается от предыдущего пошаговым достраиванием дерева решений для прогнозирования.

Вернуться в оглавление