Решающим  критерием  информативности  признаков  в  задаче распознавания образов является, конечно,  величина  потерь  от ошибок R. Даже если  распределения   генеральных совокупностей известны,  вычисление  потерь  R  связано  с  очень   большими затратами машинного времени. Поэтому применяются критерии более  просто  вычисляемые  и,  вместе  с  тем, жестко, если не однозначно, коррелированные с оценкой потерь R.  
    Если распределение реализаций каждого  образа  подчиняется нормальному  закону  с  диагональными и одинаковыми   матрицами   ковариаций (поверхности  равной  плотности   представляют  собой   сферы одинакового радиуса), то мерой  трудности  распознавания (Q) может   служить среднее значение евклидова  расстояния  между  математическими ожиданиями всех пар образов: 
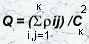  , где rij - евклидово расстояние между математическими ожиданиями i-го и j-го образов.
   В терминах теории информации мерой трудности распознавания служит энтропия H распределений плотности вероятности образов. Но в  реальных  задачах  законы распределений  реализаций  образов обычно не  известны и объем обучающей выборки  часто  бывает  небольшим.   В    этих    условиях целесообразно   использовать   методы,  которые   не   требуют построения моделей распределения  и  опираются  на  конкретные объекты, имеющиеся в обучающей выборке A. 
    По этим "прецедентам" строится решающая функция  (например, правило  k  ближайших   соседей),   распознается   контрольная последовательность и по количеству полученных ошибок выносится оценка информативности отдельного  признака  или  их  системы. Возможны и другие способы оценки информативности признаков. 
    Гипотеза  компактности  дает   нам   основу   для   оценки информативности  пространства   признаков   через   проявление характеристик компактности. Из нее следует, что  для  хорошего распознавания  образов  желательно,  чтобы  расстояния   между точками каждого образа были малыми, а расстояния между точками разных  образов  по  возможности  большими. Компактность (плотность) Di образа i, представленного в обучающей  выборке  mi  точками  1,2,...t,...l,...mi,  можно характеризовать  средней   длиной r  ребер   соединяющего  их полного графа.   Аналогично,    компактность   точек    1,2,...s,...v,...mj, представляющих образ j, будет равна  Dj . Разнесенность образов в пространстве  характеристик  можно оценивать через среднее расстояние между всеми парами точек из разных образов Dij.                  
    На основании вышесказанного  информативность  пространства признаков будет тем большей, чем больше величина