S e r g e i L' v o v i c h S o b o l e v

Key words: embedding theorems, embedding theory for abstract functions, embedding theory for spaces of differentiable functions, equations and systems unsolved for higher time derivatives,hyperbolic equations, generalized solution of a differential equation, generalized derivative, scales of functional spaces, small oscillations of rotating fluid Sobolev spaces,

Work at the Steklov Mathematical Institute

Since 1932 Sergei L'vovich worked at the Steklov Mathematical Institute in Leningrad, and since 1934, in Moscow. At that period he continued the study of hyperbolic equations. Sergei L'vovich proposed a new method to solve the Cauchy problem for a hyperbolic equation with variable coefficients which was based on a generalization of the Kirchhoff formula. Using the relations on the characteristic cone, he reduced the problem to a Volterra integral equation solvable by usual successive approximations. The new method was a development of his previous method for the Cauchy problem for the wave equation in an inhomogeneous medium. S.L.Sobolev also studied the conditions of existence of an analytic solution to the Goursat problem. The works connected with hyperbolic equations led Sergej L'vovich to revision of the classical concept of a solution to a differential equation. The concept of generalized solution of a differential equation was considered earlier by some mathematicians, e.g., N.M.Gyunter and K.O.Fridrikhs. But it was exactly in the works by S.L.Sobolev that this concept was for the first time systematically applied and thoroughly elaborated. S.L.Sobolev considered solutions in spaces of functionals, which originated the theory of distributions.

In 1933-1935 Sergei L'vovich published a series of articles on the Cauchy problem for hyperbolic equations. In these works the solvability and uniqueness of solution of the Cauchy problem in spaces of generalized functions were established. These works played an important role in development of the modern theory of partial differential equations. The apparatus of generalized functions gave rise to new methods in the theory of partial differential equations. These new methods open a way to solving many problems whose solution was long sought for, to putting many previously obtained results into a final shape, and to formulating and solving new problems. The new apparatus and related concepts and methods, which were developing especially rapidly in the 50s in the works by L.Schwartz, I. Gelfand and other researchers, changed in a short time the appearance of many sections of the theory of differential equations. Having defined the notion of generalized derivative, S.L.Sobolev introduced in mathematics spaces of functions whose generalized derivatives are integrable to some power. These objects are now called Sobolev spaces.
Let f and g be locally summable functions on an open subset G of the space Rⁿ, and let a be some multiindex. The function g is called the generalized derivative of f in the Sobolev sense or the weak derivative of order a and is denoted by D^af, if for each test function f, i.e., a function whose support of f, is compact and lies in G and f is continuously differentiable |a| = a₁+ ...+a_n times in G, the following equality holds

where D^af is the classical derivative of f of order a.
The subspace W_p^l of the vector space (classes of equivalents) of locally summable functions f on G which have in G all generalized derivatives D^af for

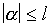
summable to the p-th power,
,
becomes a Banach space under the norm of the following form:

Sergei L'vovich found general criteria of equivalence of various norms in W_p^l and showed that statement of boundary value problems for elliptic equations is most natural in terms of these subspaces. This conclusion was based on thorough study of the properties of his spaces. The most important of these properties are embedding theorems. The essence of the embedding theorems which were established by S.L.Sobolev and became classical consists in special inequalities between the norms of one and the same function considered as an element of various spaces. The Sobolev inequalities include as special cases the integral inequalities which were established earlier by A.Poincare, V.A.Steklov, G.H.Hardy, J.E.Littlewood, et al. Basing on embedding theorems, S.L.Sobolev found a correct statement of boundary value problems for elliptic equations in multidimensional domains when boundary conditions are given on varieties of various dimensions and proved the existence and uniqueness of solutions of these problems. The embedding theory for spaces of differentiable functions created by S.L.Sobolev successfully develops. The apparatus of integral representations of functions which was extended to anisotropic cases gained further development. New scales of function spaces were found. For these function spaces new embedding theorems were established, the compactness of the embedding operator was studied, connections between various spaces were found, and the possibility of various approximations and their rate were investigated.
The apparatus of integral representations of functions, trancating and
mollifying functions, projection operators, etc. which was developed by S.L.Sobolev became classical in present-day research.

The scientific results by Sergei L'vovich brought him deserved and wide recognition. In 1933 at the age of 24 years S.L.Sobolev was elected a Corresponding Member of the Academy of Sciences, and in 1939 he became its Full Member. At that time he was and for a long time remained the youngest academician in this country.

In 1941 S.L.Sobolev was awarded the StatePrize for his works on the mathematical theory of elasticity.

In 1958 Sergei L'vovich returned once again to theory for embedding of function spaces and propounded the embedding theory for abstract functions which is closely connected with boundary value problems for quasilinear partial differential equations. Here he demonstrated a deep insight to the theory of integration of abstract functions.

A large direction in the theory of partial differential equations, asymptotic behavior of solutions to boundary value problems for nonstationary equations, was originated by Sobolev's works on almost-periodicity of solutions to the wave equation. In Sobolev's articles published in 1945 the almost-periodic was proven of solutions to the mixed problem for 2nd order equations of hyperbolic type. The almost-periodicity followed from the estimate of the integral of the sum of squared second derivatives of a solution to this problem as a function of the time. Here the embedding theorems were also applied.

In the 40s, in spired by application S.L.Sobolev began studying the system of differential equations describing small oscillations of rotating fluid. S.L.Sobolev arrived at this system when investigating the stability of a rotating body with a cavity filled with an ideal fluid. S.L.Sobolev obtained the conditions of stability of a rotating body with a cavity depending on the cavity shape and its parameters, having studied in detail the cases of a cylindrical cavity and a cavity in the form of an ellipsoid of rotation. When studying this problem, S.L.Sobolev for the first time stated and investigated the problem of the spectrum of an Hermitian operator with respect to some indefinite metric. In connection with these Sobolev's investigations there appeared one more new direction in the general theory of partial differential equations: investigation of solutions to the Cauchy problem and boundary value problems for equations and systems unsolved for higher time derivatives. For systems of such type, the questions of correctness of the Cauchy problem were studied, in particular, the conditions were found which are analogous to the Petrovskij conditions of correctness of the Cauchy problem that are setting for systems solved with respect to higher time derivatives.

Next

Top

Main

Inst. of Math.